Permutasi dan Kombinasi: Pengertian, Rumus, & Contoh Soal

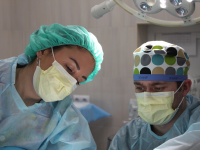
MAUKULIAH.ID – Hayo siapa di sini yang lagi pengin belajar permutasi dan kombinasi? Sini sini Miku kasih info biar gak bingung dan bisa membedakan keduanya.

Hm seperti apa penjelasan terkait permutasi dan kombinasi ini? Untuk lebih lengkapnya, yuk kita bahas bersama. 

Pengertian Permutasi

Permutasi adalah urutan yang diperhatikan Kalau masih bingung, coba Sobat Miku sedang mencatat nomor handphone seseorang, maka penting banget kan untuk memperhatikan urutan nomornya? 

Nah itu yang dinamakan permutasi, dilakukan secara urut dengan detail. Kalau gak sesuai urutannya, bisa jadi nomor handphone-nya jadi salah deh.

Dalam matematika, permutasi ini merupakan urutan elemen-elemen dari sebuah himpunan. Ini menunjukkan berapa banyak cara yang mungkin untuk mengatur elemen-elemen tersebut. Permutasi sering digunakan ketika urutan atau susunan dari elemen-elemen tersebut penting.

Misalnya, Sobat Miku memiliki himpunan {A, B, C}, permutasi dari himpunan ini akan menunjukkan berapa banyak cara yang berbeda untuk mengatur elemen-elemen tersebut, seperti ABC, ACB, BAC, dll. 

Baca juga: Mengenal Jurusan Pendidikan Bahasa Arab, Mata Kuliah, & Prospek

Pengertian Kombinasi

Terus bedanya permutasi sama kombinasi apa dong? Kombinasi ini urutannya acak. Coba deh perhatikan orang-orang yang beli mangga 1kg, mereka mengambil mangga dengan acak tanpa memperhatikan berat per mangga. Intinya berat mangga itu harus 1 kg, gak peduli berat per mangga itu ukurannya berapa.

Jadi, kombinasi ini berkaitan dengan cara memilih elemen-elemen dari sebuah himpunan tanpa memperhatikan urutan. Jadi kombinasi ini dipilih tanpa memperhatikan posisi relatif satu sama lain.

Misalnya, dari himpunan {A, B, C}, kombinasi ini akan memberi tahu berapa banyak cara yang mungkin untuk memilih elemen dari himpunan tersebut tanpa memperhatikan urutan. Jadi, ABC dan CBA dianggap sebagai satu kombinasi yang sama.

Perlu Sobat Miku ketahui, ada dua jenis kombinasi yang dapat terjadi:

1. Kombinasi dengan pengulangan: Sebagai contoh, ketika seseorang mengambil 3 bola dari suatu wadah yang memuat 3 bola merah dan 3 bola biru, mungkin hasilnya adalah 2 bola merah dan 1 bola biru.
2. Kombinasi tanpa pengulangan: Sebagai contoh lain, ketika seseorang memilih 2 individu dari sebuah kelompok yang terdiri dari 5 orang, tidak mungkin individu pertama dan kedua merupakan orang yang sama.

Agar memudahkan Sobat Miku menjumlahkan bilangan permutasi dan kombinasi, berikut Miku bahas rumus permutasi dan kombinasi yang lengkap dengan soalnya. 

Rumus Permutasi dan Kombinasi

Rumus Permutasi

1. Untuk himpunan dengan n elemen yang berbeda, jika diambil n unsur, jumlah susunan yang berbeda dari himpunan tersebut adalah:

Keterangan:

P: banyaknya permutasi

n: banyaknya elemen himpunan keseluruhan

r: banyaknya elemen himpunan yang diamati

Contoh soal

Ada 4 orang siswa, yaitu A, B, C, dan D, yang akan duduk di bangku yang berurutan. Berapa banyak susunan duduk yang dapat dibentuk?

Pembahasan

n = jumlah benda 

P = permutasi 

n! = jumlah benda faktorial.

Dalam soal ini, n = 4, sehingga nPn = 4!.

4! = 4 x 3 x 2 x 1 = 24

Jadi, banyak susunan duduk yang dapat dibentuk adalah 24.

2. Untuk setiap bilangan positif n dan r, di mana r ≤ n, jumlah permutasi dari n objek yang diambil r objek pada satu waktu adalah:

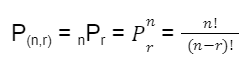
Contoh soal:

Sebuah toko roti memiliki 10 jenis roti yang berbeda. Berapa banyak cara untuk memilih 3 jenis roti untuk dijual?

Pembahasan:

Dalam soal ini, n = 10, dan r = 3.

P(10,3) = 10!/(10-3)! = 10 x 9 x 8 x 7 / 7! = 120

Jadi, ada 120 cara untuk memilih 3 jenis roti untuk dijual.

Jawaban: 120

3. Permutasi dari himpunan n unsur yang memuat p, q, dan r unsur yang sama adalah:

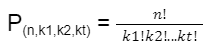
Keterangan:

n    = banyaknya elemen seluruhnya

k1  = banyaknya elemen kelompok 1 yang sama

k2  = banyaknya elemen kelompok 2 yang sama

kt   = banyaknya elemen kelompok kt yang sama

t = 1,2,3,…

Contoh soal:

Ada 7 huruf, yaitu 3 huruf A, 2 huruf B, dan 2 huruf C. Berapa banyak susunan huruf yang dapat dibentuk?

Pembahasan:

n = 7, p = 3, q = 2, r = 2

P(n, pqr) = n! / p!q!r! = 7! / 3!2!2! = 210

Jadi, ada 210 susunan huruf yang dapat dibentuk.

4. Permutasi siklis merujuk pada permutasi yang terjadi dalam urutan melingkar.

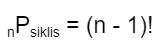
Keterangan:

P: permutasi. 

n: banyaknya unsur 

!: lambang faktorial

Contoh soal

Sebuah roda berputar memiliki 12 jari-jari. Berapa banyak susunan jari-jari yang dapat dibentuk jika jari-jari tersebut tidak dapat dipindahkan?

Pembahasan:

Dalam soal ini, n = 12, dan posisi jari-jari melingkar, sehingga P(n,n) tidak berlaku. Yang berlaku adalah rumus permutasi siklis, yaitu:

Ps(n) = (n-1)!

Ps(12) = (12-1)! = 11! = 39916800

Jadi, ada 39916800 susunan jari-jari yang dapat dibentuk.

5. Permutasi berulang dari n unsur, di mana tipe permutasinya terdiri dari k unsur, menjelaskan jumlah cara di mana k unsur dapat diatur ulang dari n unsur yang sama.

Soal:

Ada 5 bola merah yang identik. Berapa banyak cara untuk mengatur ulang 3 bola merah dari 5 bola tersebut?

Pembahasan:

Dalam soal ini, n = 5, dan k = 3.

Permutasi berulang dari n unsur, di mana tipe permutasinya terdiri dari k unsur, dapat dihitung dengan rumus berikut:

P(n,k) = (n-k)!

P(5,3) = (5-3)! = 2! = 2

Jadi, ada 2 cara untuk mengatur ulang 3 bola merah dari 5 bola tersebut.

Rumus Kombinasi

Keterangan:

C = kombinasi

n = jumlah kejadian yang bisa dipilih

r = jumlah kejadian yang harus dipilih

! = simbol faktorial

Contoh soal

Sebuah tim sepak bola terdiri dari 11 pemain. Berapa banyak cara untuk memilih 5 pemain untuk memulai pertandingan?

Pembahasan:
Dalam soal ini, n = 11, dan r = 5.
C(11,5) = 11! / (5!(11-5)!) = 11 x 10 x 9 x 8 x 7 / 5 x 4 x 3 x 2 x 1 = 462

Jadi, ada 462 cara untuk memilih 5 pemain untuk memulai pertandingan.

Baca juga: 10 Rekomendasi Universitas Terbaik di Yogyakarta

Nah itu tadi penjelasan lengkap mengenai permutasi dan kombinasi beserta contohnya. Semoga dapat membantu Sobat Miku ya untuk memahami materi ini. Buat Sobat Miku yang ingin mencari informasi terkait materi sekolah dan jurusan, jangan lupa kunjungi maukuliah.id ya!

Sumber: Pixabay